Leibniz’s Lost Language – ‘Characteristica Geometrica’ and the Symbolic Art of Mathematics

Matthew McMillan is Assistant Professor of Applied Mathematics at the University of Virginia School of Engineering and Applied Science. He is translating G. W. Leibniz’s writings and building a modern analogue of Leibniz's encyclopedia for math students. He discovered Leibniz’s philosophy and ideas for mathematical language while at Oxford as a Marshall Scholar in 2016. McMillan obtained his PhD in pure mathematics from the University of California, Los Angeles, where his work focused on categorical representation theory, a subject that employs the language of abstract algebra as a bridge from quantum physics to mathematical topology.

Gottfried Wilhelm Leibniz was a German polymath best known for his invention of calculus (in mathematics) and his thesis that God created the “best of all possible worlds” (in philosophy). A synthesis of rationalism and humanism marked his approach to philosophy. His rationalism meant a focus on the production and analysis of reasons for everything, leading to work towards mechanical calculators for knowledge of all kinds. His humanism involved his belief in the fundamentality of the organic, both in his abstract metaphysics, in which he argued that living beings logically precede their material composition, and in his working method, where he considered the historical origins and evolution across epochs for everything he studied and set the betterment of humanity as the goal of his inventions.

Leibniz sought to create a “universal encyclopedia” of all human knowledge. Just as for his mechanical computer and fascination with binary numbers, his vision for this encyclopedia vastly outstripped the technical capacities of his time. Alongside it, he wished to design a type of symbolic-algebraic artificial language which would more naturally express the concepts in the encyclopedia and the structure of their interrelations. This language would allow us (he hoped) to manipulate mathematical knowledge more intuitively and efficiently, enabling non-experts to apply the products of scholarship without the deep understanding required to discover them.

Leibnizean Language and Geometry

The best-known example of Leibniz’s work on artificial language is, of course, the calculus familiar to first-year college students. His invention of infinitesimal notation, as in "dy/dx", or the integral “S” sign, as in “ ∫ f(x) dx”, is partly responsible for the success of calculus and (as he believed) the possibility of its use by practicing engineers and not just the Isaac Newton’s of the world.

Less well-known is Leibniz’s project to reform geometry. Just before Leibniz’s time, the great Descartes invented and promoted a new approach to geometry in which shapes are first reduced to numbers and then analyzed in terms of numbers using the systems of arithmetic and algebra. Think of the familiar Cartesian coordinate plane, with its points, lines, and circles:

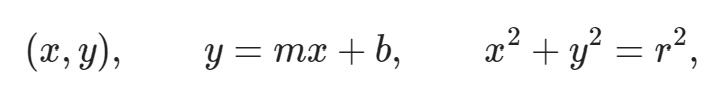
each described using algebraic variables and equations. Leibniz opposed the Cartesian school of thought because he believed the language of numbers was not properly tailored to geometric forms (i.e. structures), and he feared that overindulgence in Cartesianism could lead to forgetfulness of the questions and goals that genuinely belong to geometry. So, Leibniz set out to create his own alternative system, which he dubbed the ‘characteristica geometrica,’ the symbolic art of a subject he called analysis of situation.

The Task of Translation

Leibniz’s writings on characteristica geometrica are almost entirely untranslated into English. He did not publish this work during his lifetime after an initial essay sent to the eminent Dutch polymath Christiaan Huygens was misunderstood and rebuffed. Leibniz’s contemporaries and subsequent scholars, from Kant to Poincaré, learned about this project through cryptic references to it that Leibniz included in correspondences.

A series of key essays he wrote on this topic were discovered in Leibniz’s enormous manuscript collection, which I have turned into a book project with my collaborator David Jekel. Each translation task comes with unique challenges. Sometimes, forms of expression rely on specific features of a language, such as the way it sounds, for example, in rhyming or metered poetry, and these can be extremely difficult to replicate in another language. In the case of Leibniz’s writings on characteristica geometrica, our main challenge comes from the evolution of mathematical idiom from its very nascent form in Leibniz’s day to a more crystallized set of conventions used today.

Mathematical idioms are English phrases and patterns that are used to express specific and sometimes technical thoughts or maneuvers in mathematical argumentation. They work by resonating in the reader’s mind with familiar maneuvers, with steps that have been analyzed and digested in the past and now are received through idiom as through a kind of shorthand.

Leibniz was writing near the beginning of the modern math period and used phrases that evolved into modern idioms only later. The meaning of these phrases in his day is still a more literal kind. As such, these phrases sometimes draw connections to broader philosophical concepts. The translation challenge, then, is that of deciding whether to render a given phrase in the modern idiomatic form that became a sort of crystallization of the old phrase and, in doing so, to connect better with modern mathematician readers, or instead to break the modern idiom intentionally, using a non-standard word choice or word order, thereby enabling readers to notice the etymological origins of the separate words and to have a chance of perceiving philosophical-conceptual aspects that would have been forefront in Leibniz’s mind.

While translation work can feel unrewarding in various ways, there is satisfaction in serving as the intermediary for and advocate of Leibniz’s long-lost language of space through a translation that may be relied upon for generations to come. It is an exciting time for Leibniz scholarship! The Leibniz Archiv in Hanover has finally reached these texts in their process of creating studied transcriptions, and a research center in Paris is currently working to reassess Leibniz’s mathematical papers in the light of many newly documented manuscripts. It is a great pleasure to take part in the active collegial exchange in these communities and contribute my understanding of Leibniz's ideas in the English language.